Introdução à Programação Funcional,
em OCaml
Ficha Prática
Simão Melo de Sousa |
Esta ficha prática introduz um conjunto de exercícios que visam a
aquisição de conhecimento básico da programação funcional em OCaml
Contents
1 Exercício : Digressões sobre a sequência de Fibonacci
O objectivo deste exercício é escrever um programa Ocaml que permita
calcular para um dado n∈ ℕ o valor de Fib(n), tendo
em conta que :
| | Fib(0) = 1 |
| Fib(1) = 1 |
| Fib(n+2) = Fib(n) + Fib(n+1)
|
|
|
-
Numa primeira abordagem, escreva um programa que peça o valor de
n via menu. O calculo deverá ser feito de forma recursiva;
- modifique o seu programa de forma a que o valor de n seja dado
pela linha de comando;
- modifique o seu programa de forma a que o valor de n seja
extraído de um ficheiro chamado dados.txt;
- calcule fib(42) e fib(50). Explique o resultado;
- dê uma versão iterativa do calculo de Fib(n);
- dê uma versão recursiva terminal do calculo de Fib(n);
- dê uma versão com memoization da função Fib(n);
- considere a propriedade seguinte da sequência de fibonacci
|
=
| ⎡
⎢
⎣ | | Fib n | Fib (n −1) |
| Fib (n−1) | Fib (n−2)
|
| ⎤
⎥
⎦ |
|
Tenha em consideração a propriedade seguinte da exponenciação de
matrizes quadradas M por um inteiro n:
Quando bem usada, esta propriedade permite uma exponenciação em
tempo logarítmico.
Dê uma versão da função fibonacci que tire proveito desta propriedade;
- calcule fib(10000) com esta última solução;
- o problema com as duas últimas soluções para sequência de Fibonacci é a
conjunção das suas capacidades melhorada em calcular valores da função fibonacci com o
uso do tipo inteiro int. Estes valores rapidamente
ultrapassam a capacidade do tipo int.
Altere a resolução anterior para que se use o módulo Num (módulo OCaml com tipos de dados e
operações para a aritmetica de precisão arbitrária).
2 Exercício : Cálculos sobre Polinómios de uma variável - Método de Horner e derivação
Podemos representar um polinómio P de grau n por uma lista p
de reais em o i-ésimo elemento da lista representa o coeficiente
associado é potência de grau i.
Assim, a título de exemplo, o polinómio 3x4+5x2+1 é
dado pela lista [3.;0.;5.;0.;1.] (ou [1.;0.;5.;0.;3.], se
preferirmos que o polinómio seja listado do grau mais fraco ao grau
mais forte).
-
Escreva uma função que peça o
valor de n (com a restrição que n≥ 0) e inicialize P (lê os
diferentes coeficientes ai, onde 0≤ i ≤ n);
- escreva uma função de escrita/visualização (output) que dado um polinómio
p na sua forma de lista permite a sua visualização no
standard output.
Considere polinómio x5+3x4+5x2. Este polinómio representa-se
pela lista [1.;3.;0.;5.;0.;0.]. A função deverá ser capaz de
reproduzir a string "x^5+3.x^4+5.x^2" (com mais ou
menos decimais);
- escreva uma função recursiva que
dado um x, calcule P(x) usando o método de Horner, i.e.
| Pn(x)=(⋯((an x + an−1)x + an−2)x + ⋯ + a1)x + a0
|
- escreva uma função que, dado um polinómio P(x) dado na forma de
uma lista, calcula o polinómio derivada de P em x;
- se a solução do ponto anterior não estiver numa forma recursiva
terminal, proponha uma solução que o seja.
3 Exercício : Listas e sub-listas
-
Define a função sublista l que calcula a lista de todas as sublistas de l
com os elementos na ordem presente na lista original (ou seja
[a;c] é sublista de [a;b;c] mas não [c;a]).
Por exemplo:
sublista [a;b;c]= [[];[c];[b];[b;c];[a];[a;c];[a;b];[a;b;c]]
- Define a função insertion e l que calcula a lista de todas as listas possíveis que resultam da
inserção de e em l.
Por exemplo:
insertions e [a;b;c] =
[[e;a;b;c];[a;e;b;c];[a;b;e;c];[a;b;c;e]]
- Define a função permutation l que calcula a lista de todas as permutações de l.
Por exemplo:
permutation [a;b;c] = [[a;b;c];[b;a;c];[b;c;a];[a;c;b];
[c;a;b]; [c;b;a]]
- Define a função subbag l que calcula a lista de todas as permutações de todas as
sublistas de l. Pretendemos gerar todas as sublistas possíveis duma determinada lista. Este
exercício assemelha-se à geração do conjunto de todos os subconjuntos
dum determinado conjunto com a particularidade de que a ordem dos elementos importa
(a lista [a;b] é diferente da lista [b;a] e pretendemos aqui
considera-las ambas). Por exemplo:
subbag [a;b;c] = [[]; [a]; [b]; [c]; [a;b]; [a;c] ; [b;a] ; [b;c]
; [c;a] ; [c;b] ; [a;b;c]; [a;c;b] ; [b;a;c] ; [b;c;a]; [c;b;a] ;
[c;a;b]]
4 Exercício : Códigos de Gray
Os códigos de Gray permitam uma codificação binária cómoda em que um
só bit difere entre elementos consecutivos.
Para simplificar, iremos nos restringir ao caso dos inteiros.
Neste caso, a codificação de 0 é 0 e a codificação de 1 á 1.
A codificação de 17 é 11001, a codificação de 18 é 11011 e a
codificação de 19 é 11010.
Uma forma simples de gerar os códigos de gray dos valores inteiros até ao
tamanho n (por exemplo 19 tem uma codificação de tamanho 5) é
designada de método reflex-and-prefix.
Este método é explicado pela imagem da figura 1 (fonte : wikipedia)
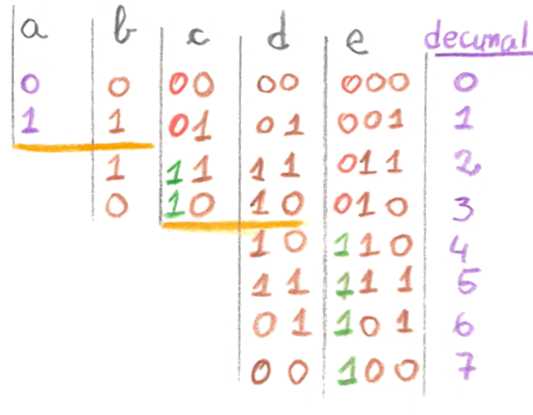
| Figure 1: Código de Gray: Método reflex and prefix |
Legenda da figura 1 :
-
coluna a : código gray de 1 bit
- coluna b: reflexão do código (traço laranja)
- coluna c: adicionar 0 à cabeça de todos os códigos acima do eixo de
reflexão e 1 a todos os que estão por baixo. Obtemos um código de 2 bits
- coluna d: reflexão do código da coluna anterior para esta coluna,
tendo em conta o eixo de reflexão discriminado a laranja.
- coluna e: adicionar 0 à cabeça de todos os códigos acima do eixo de
reflexão e 1 a todos os que estão por baixo. Obtemos um código de 3
bits que consegue representação dos inteiros de 0 a 7.
-
Define uma função que dado um n calcula todos os códigos de
gray de tamanho n. Estes código são devolvidos na forma de uma lista;
- define uma função que dá o código de gray de um determinado
inteiro n em parâmetro.
5 Exercício : Sorteio do totoloto
Neste exercício vamos simular um sorteio do totoloto.
-
Codificar a grelha como uma matriz 7 × 7 de booleanos;
- definir uma função que preencha a grelha a partir de uma
sequência de 7 números distintos (entre 1 e 49);
- definir uma função que dado um sorteio (lista de 6 números
inteiros complementado com um inteiro – o complementar) diz em quantos números se acertou.
6 Exercício : Digressões sobre árvores AVL
Neste exercício vamos redescobrir uma estrutura de dados clássica,
as árvores AVL que são árvores binárias ordenadas e equilibradas.
-
Define o tipo (polimórfico) das árvores binárias
eventualmente vazias com a informação da altura em cada nodo (por
exemplo uma árvore de altura x tem esta informação arquivada na raiz);
- define as funções altura (que calcula a altura de uma árvore),
folhas (que calcule o número de folhas de uma árvore) e nodos (que
calcula o número total de nós de uma árvore, folhas incluidas);
- define a função fold_dfs f init ar que, a
semelhança do fold_left para as listas aplica uma função binária f a
todos os elementos da árvore ar usando a estratégia dfs
(depth-first-search, em
profundidade primeiro, da esquerda para a direita). O valor
inicial do acumulador (que acumula o resultado da função f no
percurso dfs) é init;
- define igualmente a função map f ar sobre as árvores;
- define a função fold_bfs f init ar (breadth-first
search, em largura primeiro, da esquerda para a diteita) que aplica
a função binária f a todos os elementos da árvore
ar. O valor inicial do acumulador é init;
- proponha uma versão recursiva terminal de fold_dfs e de fold_bfs;
- define as funções de rotação balanceLL, balanceLR, balanceRL e
balanceRR que calculam as rotações equilibradas esquerda-esquerda
(resp. esquerda-direita, direita-esquerda e direita-direita );
- define uma função insert e ar que insere o elemento e ordenadamente
e de forma equilibrada na árvore ar;
- define uma função remove e ar que remove o elemento e ordenadamente
e de forma equilibrada da árvore ar.
7 Exercício : Fórmulas lógicas proposicionais e Forma Normal
Conjuntiva
O objectivo deste exercício é a exploração dos tipos soma. No caso
particular deste exercício do tipo das expressões lógicas (proposicionais).
-
Define o tipo das expressões lógicas proposicionais;
- define o tipo das formas normais conjuntivas (FNC);
- implemente o algoritmo T que permite a conversão de
uma fórmula lógica proposicional para FNC;
- proponha uma implementação do algoritmo de Horn.
This document was translated from LATEX by
HEVEA.