Ficha OCaml 5: Listas e vetores
Ficha OCaml 5: Listas e vetoresNível BásicoEx. Utilitários sobre listas.Ex. Brilhar em sociedade.Ex. Totoloto.Ex. Ordenar listas ou vetores com critério.Ex. Em caso de litígio, cortar ao meio.Nível IntermédioEx. Cálculos sobre Polinómios de uma variável - Método de Horner e derivação.Ex. RLE.Ex. Sequência máxima de true.Ex. Listas e sub-listas.Ex. Randomness is hard!Ex. Zombie Attack!Ex. Maioria absoluta!Ex. O problema da bandeira holandesa.Ex. Códigos de Gray.Ex. Problema da sublista máxima.Nível ConsolidadoEx. subsequência de listas.Ex. Parentesar bem.Ex. A transformada de Burrows-Wheeler.Ex. Crise de petróleo.Ex. Luigi’s Pizzeria - From MIUP 2018.
Nível Básico
Ex. Utilitários sobre listas.
Define as seguintes funções sobre listas:
a função
soma : int list -> intque devolve a soma dos inteiros contidos na lista em parâmetro.Por exemplo,
soma [1;5;3]devolve9;a função
conta_pares : int list -> intque devolve a quantidades de pares presentes na lista de inteiros em parâmetro. Por exemploconta_pares [1;-6;3;17;4;80;-18]devolve4;a função booleana
palindroma : 'a list -> bool, que devolvetruese a lista em parâmetro é um palíndroma,falsesenão. Por exemplopalindroma ['a';'t';'d';'d';'t';'a'], oupalindroma [1;5;3;5;1]devolvemtrue;a função
maiusculas : char list -> char listque transforma cada caracter da lista que seja uma letra minúscula para uma letra maiúscula. Por exemplomaiusculas ['a';'9';'T';'%';'z';'-']devolve['A';'9';'T';%';'Z';'-'];a função booleana
is sorted : 'a list -> ('a -> 'a -> int) -> bool, que devolvetruese a lista em parâmetro é ordenada conforme critério de ordenação indicado pelo segundo parâmetro.Assim,
is_sorted [1;3;7;9] comparedevolvetrue,is_sorted [1;3;7;9] (fun a b -> compare b a)devolvefalse. Relembramos que a função compare da biblioteca standard OCaml é definida como:-
compare a b = -1se a<b-
compare a b = 1se a>b-
compare a b = 0se a=ba função
remove_duplicate_sorted :'a list -> 'a listque remove os elementos duplicados de uma lista que se assume estar ordenada. Por exemploremove_duplicate_sorted [1;1;2;2;3,5;5;6;7;8;8;8;9] = [1;2;3;5,6;7;8;9].a função
remove_ duplicate : 'a list -> 'a listque remove os elementos duplicados de uma lista. Não se assume que esta esteja ordenada.remove_duplicate [9;1;7;6;6;7;8;1;2;6;2;3,5;5;1;9] = [1;2;3;5,6;7;8;9].
Tente, o quanto possível, usar os combinadores sobre listas (fold_left, map, for_all, iter, exists, filter, etc. )
Ex. Brilhar em sociedade.
Afinal, brilhar num jantar é fácil, ser a estrela de um vernissage é tão fácil como comer um canapé. Basta aplicar esta receita infalível. Selecionar ao acaso um elemento de cada coluna aqui listada e juntar na ordem dos conjuntos para formar uma frase... et voilá.
Por exemplo, "O diagnóstico identifica os bloqueios institucionais da prática comum".
| Conjunto 1 | Conjunto 2 | Conjunto 3 | Conjunto 4 | Conjunto 5 |
|---|---|---|---|---|
| "A excelência" | "reforça" | "os fatores" | "institucionais" | "do desempenho"; |
| "A intervenção" | "mobiliza" | "os processos" | "organizacionais" | "do dispositivo" |
| "O objetivo" | "revela" | "os parâmetros" | "qualitativos" | "da empresa" |
| "O diagnóstico" | "estimula" | "os progressos" | "analíticos" | "do grupo" |
| "A experimentação" | "modifica" | "os conceitos" | "característicos" | "dos beneficiários" |
| "A formação" | "clarifica" | "os diferentes know-how" | "motivacionais" | "da hierarquia" |
| "A avaliação" | "renova" | "os problemas" | "pedagógicos" | "da prática comum" |
| "A finalidade" | "identifica" | "os indicadores" | "representativos" | "dos procedimentos" |
| "A expressão" | "aperfeiçoa" | "os resultados" | "contributivos" | "dos atores" |
| "O management" | "desenvolve" | "os efeitos"; | "cumulativos"; | "da problemática" |
| "O método" | "dinamiza" | "os bloqueios" | "estratégicos" | "das estruturas" |
| "A vivência" | "programa" | "os pré-requisitos" | "neuro-linguísticos" | "do meta-contexto" |
| "O reenquadramento" | "pontua" | "os paradoxos" | "sistémicos" | "da organização" |
Assuma que cada conjunto está organizado na forma de um vetor declarado como global, concretamente v1, v2, v3, v4 e v5.
Implemente uma função
falar_vacuosamente : unit -> stringque produz uma tal frase aleatoriamente.Para esse efeito poderá auxiliar-se da função
Random.intdo módulo OCamlRandom(ver https://caml.inria.fr/pub/docs/manual-ocaml/libref/Random.html) :Random.int : int -> intRandom.int boundreturns a random integer between (inclusive) andbound(exclusive).boundmust be greater than and less than .Com o recurso desta função poderá sortear inteiros pertencentes ao intervalo . Tenha em atenção que não é esperado que use funções como
Random.initouRandom.self_init.
Ex. Totoloto.
Neste exercício vamos simular um sorteio do totoloto.
Define o tipo
grelhascomo sendo o tipo das matrizes de booleanos.Define uma função
make_grelhaque dado um inteirondevolve uma grelha de tamanho inicializada com o valorFalse.Define uma variável global
grelhade tipogrelhascomo sendo uma grelha .Define uma função
fill: int list -> grelhaque, dada uma lista de inteiros distintos compreendidos entre e , cria e preencha uma grelha que é no final devolvida. Na grelha, um valor do sorteio encontra-se com o valortrue.Definir uma função
sorteio : grelha -> int list -> int -> (int list * bool)que dado um sorteio (lista de números inteiros complementado com um inteiro -- o complementar) diz em quantos números se acertou, complementar incluído.Por exemplo se o sorteio for , , , , e e o número complementar for , e se a
grelhaem parâmetro contemplar , e , então a resposta asorteio grelha [1;5;23;30;31;45] 17deverá ser([1;30],true)que significa "acertou no e no , e também no complementar".
Ex. Ordenar listas ou vetores com critério.
Pretendemos trabalhar com listas ou vetores de inteiros. Neste contexto queremos ordenar uma lista de inteiros com recurso às funções List.sort ou Array.sort e usando vários critérios:
Escrever a função
sort1 : int array -> unitque ordena o vetor em parâmetro de forma decrescente usando a funçãoArray.sort.Escrever a função
sort2 : int list -> int listque ordena a lista em parâmetro usando a funçãoList.sorte o critério de ordenação seguinte:1- primeiros os inteiros impares (são considerados menores do que os inteiros pares), seguem os pares;2- nos inteiros impares, a regra de comparação é a ordem decrescentes;3- no inteiros pares a ordem é crescente.Escrever a função
sort3 : array list -> unitque ordena o vetor em parâmetro usando o critério da alínea anterior mas com recurso, claro, à funçãoArray.sort.Escrever uma função
sort4 : int list -> int listque ordena os inteiros da lista em parâmetro por ordem lexicográfica dos seus valores lidos ao contrário. Por exemplo consideremos e . Lidos da direita para a esquerda temos de comparar com . Como é maior, nesta ordem particular. Espera-se, novamente, que use a funçãoList.sort.Assim
sort4 [121;17;191;32;19;91]devolve[121;91;191;32;17;19].
Ex. Em caso de litígio, cortar ao meio.
Defina uma função halve : 'a list -> ('a list * 'a list') que corta a lista que recebe ao meio. Em caso de lista de comprimento impar, o elemento do meio fica na lista da direita .
Assim, halve [1;2;3;4;5;6;7;8;9] = ([1;2;3;4],[5;6;7;8;9]).
De notar que existe uma resolução que usa uma função auxiliar recursivas terminal (com mais parâmetros do que halve), que só precisa de percorrer a lista completa uma vez e uma vez a primeira metade.
Nível Intermédio
Ex. Cálculos sobre Polinómios de uma variável - Método de Horner e derivação.
Podemos representar um polinómio de grau por uma lista de reais em o -ésimo elemento da lista representa o coeficiente associado à potência de grau .
Assim, a título de exemplo, o polinómio é dado pela lista [3;0;5;0;1] (ou [1;0;5;0;3], se preferirmos que o polinómio seja listado do grau mais fraco ao grau mais forte). Vamos assumir neste exercício que preferimos o grau mais forte à esquerda.
- Define o tipo
polinoniocomo sendo uma lista de reais em par com um inteiro que representa o grau máximo deste polinómio. Usando o exemplo acima descrito, um valor de tipopolinómioé(4,[3;0;5;0;1]). - Escreva uma função
horner : float -> polinomio -> floatque dado um , calcule usando o método de Horner, i.e.
Assim horner 3.0 (4,[3;0;5;0;1]) devolve 289.0.
Escreva uma função
deriva : polinomio -> polinomioque, dado um polinómio dado na forma de uma lista, calcula o polinómio derivada de em .deriva (4,[3;0;5;0;1])devolve(3,[12;0;10;0]).Proponha nesta alínea uma versão recursiva terminal
deriva_rt : polinomio -> polinomio -> polinomioda funçãoderiva.
Ex. RLE.
Propomos neste exercício programar um método de compactação clássica e simples, designado de run-length encoder (RLE).
Este método permite compactar sequências de elementos atuando sobre as subsequências que são repetições do mesmo elemento.
É eficaz quando as sequências consideradas têm tendências em conter muitas ocorrências repetidas. Por exemplo é usada com conjunto com outros métodos de compactação que originam tais repetições (o método de Burrows-Wheeler) , na compactação de imagens, nalguns FAX, etc.
Para exemplificar utilizaremos listas de caracteres, mas o método funciona para sequências de qualquer tipo.
Assim aaiojanbeeebbaffssjjjjdreghsrf pode ser compactado em a2iojanbe3b2af2s2j4dreghsrf.
A regra simples é que cada subsequência de um caracter, digamos x, de comprimento y é substituída por xy que significa "x, y vezes". A codificação RLE é a simples aplicação desta regra básica. A descodificação, que permite obter o texto original, reverte trivialmente este processo.
Dado um elemento
xde uma lista por compactar, pretendemos definir a sua imagem pela codificação RLE. Se for uma ocorrência única então pretendemos que a codificação retorneOne x, se for o primeiro elemento de uma repetição de comprimentoy, então pretendemos que a codificação devolvaMany (x,y).Defina o tipo
rle_contentsdo conteúdo de uma lista proveniente de uma codificação RLE, sabendo que a lista por codificar é uma lista qualquer (de tipo'a list).Defina a função
rle_encode : 'a list -> 'a rle_contents listque calcula a codificação da lista em parâmetro. Por exemplorle_encode [1;1;3;3,3;2;5;5]devolve[Many (1,2); Many (3,3); One 2; Many (5,2)].Define a função inversa,
rle_decode : 'a rle_contents list -> 'a list.
Ex. Sequência máxima de true.
Usando um iterador (e.g. fold_left, map, for_all, iter, exists, filter, etc. ) definir uma função max_seq : bool list -> int que devolve o comprimento da maior sequência de valores true de uma lista de booleanos dada em parâmetro. Por exemplo max_seq [true;true; false ; true; false; true ; true; true: true; false;false;true] devolve .
Ex. Listas e sub-listas.
Pretendemos definir a função
subslita: 'a list -> 'a list listque permite calcular a lista de todas as sublistas de uma listalcom os elementos apresentados na ordem da lista originall.Por exemplo
sublista [a;b;c]=[[];[c];[b];[b;c];[a];[a;c];[a;b];[a;b;c]]ou ainda,[a;c]é sublista de[a;b;c]mas não[c;a].- Qual é o resultado esperado para
sublista []? - Qual é o resultado esperado para
sublista [c]? - Qual é o resultado esperado para
sublista [b;c]? - Que padrão recursivo para a função
sublistapodemos inferir destes exemplos anteriores? - Define a função
sublista : 'a list -> 'a list list.
- Qual é o resultado esperado para
Pretendemos definir a função
subslita: 'a -> 'a list -> 'a list listque permite calcular todas as formas de inserir um elementoenuma listal. Assim inserirena lista[a;b;c]pode resultar nas listas seguintes:[e;a;b;c][a;e;b;c][a;b;e;c][a;b;c;e]
- Qual é o resultado esperado para
insertion e []? - Qual é o resultado esperado para
insertion e [c]? - Qual é o resultado esperado para
insertion e [b;c]? - Que padrão recursivo para a função
insertionpodemos inferir destes exemplos anteriores? - Define a função
insertion e : 'a -> 'a list -> 'a list list.
Vamos agora definir a função
permutationque calcula a lista de todas as permutações do seu parâmetro listal. Por exemplopermutation [a;b;c] = [[a;b;c];[b;a;c];[b;c;a];[a;c;b];[c;a;b]; [c;b;a]]- Qual é o resultado esperado para
permutation []? - Qual é o resultado esperado para
permutation [c]? - Qual é o resultado esperado para
permutation [b;c]? - Que padrão recursivo para a função
permutationpodemos inferir destes exemplos anteriores? - Define a função
permutation : a list -> 'a list list.
- Qual é o resultado esperado para
Finalmente queremos definir
subbag lque calcula a lista de todas as permutações de todas as sublistas del. Por exemplo,subbag [a;b;c]= [[]; [a]; [b]; [c]; [a;b]; [a;c] ; [b;a] ; [b;c] ; [c;a] ; [c;b] ; [a;b;c]; [a;c;b] ; [b;a;c] ; [b;c;a]; [c;b;a] ; [c;a;b]].O que esta função calcula é algo de mais "explosivo" do que o conjunto de todos os subconjuntos de uma determinado conjunto (ou lista), tendo em conta que a ordem é relevante (
[a;b][b;a]).- Define a função
subbag : a list -> 'a list listtendo em conta as funções da alíneas anteriores. - Não haverá forma de definir a função
subbagdiretamente, sem recorrer às funções das alíneas anteriores? Para tal Use a metodologia incremental sugerida nas alíneas anteriores para extrair um padrão que se possa programar.
- Define a função
Ex. Randomness is hard!
O problema que vamos resolver aqui resume-se na questão seguinte:
Tendo um vetor v de dimensão n previamente inicializado, como misturar os seus elementos de uma forma simples (i.e. não muito custosa) e obter um uma mistura bem feita ?
Isto é, como obter uma permutação dos seu elementos que pareça realmente aleatória ?
O problema levantado por esta questão parece simples, mas não. Não é imediato calcular de forma simples uma permutação que tenha boas propriedades de aleatoriedade.
Ronald Fisher e Frank Yates descreveram em 1938 no livro Statistical tables for biological, agricultural and medical research um método que foi depois estudado e popularizado pelo próprio Donald Knuth, himself...
Este método ficou conhecido como o Knuth shuffle ou Fisher-Yates-Knuth shuffle.
xxxxxxxxxx41Para misturar um vetor v de n elementos (índices 0..n-1) fazer:2 para i de n - 1 até 1 fazer3 j = inteiro aleatório que verifica 0 <= j <= i4 trocar v[j] e v[i]A propriedade essencial que este método garante é a de que qualquer permutação possível tem a mesma probabilidade em ser obtida por este método, inclusive o próprio vetor original.
Define a função knuth_shuffle: 'a array -> unit que implemente o algoritmo acima apresentado. Tenha em atenção que o argumento é o vetor por misturar. Os valores aleatórios poderão ser obtidos com o recurso à função Random.int do módulo OCaml Random (ver https://caml.inria.fr/pub/docs/manual-ocaml/libref/Random.html) :
Random.int : int -> int
Random.int boundreturns a random integer between (inclusive) andbound(exclusive).boundmust be greater than and less than .
Tenha em atenção que não é esperado que use funções como Random.init ou Random.self_init .
Ex. Zombie Attack!
O seu bairro sofreu uma invasões de zombies. Não fossem os gatos, naturalmente imunes a doença e predadores dos zombies, o seu bairro estava condenado.
O bairro tem a forma de um tabuleiro de n por n e cada célula do tabuleiro tem alternativamente uma pessoa, um gato ou um zombie.
Um zombie ataca os seus vizinhos de cima, de baixo, da direita e da esquerda. Quando um homem é atacado por um zombie, este transforma-se em zombie e ataca de seguida os seus vizinhos (mais uma vez, os de cima, baixo, esquerda e direita). Quando um gato é atacado, este simplesmente anula o ataque e fica como tal, um gato. Quando um zombie é atacado por outro zombie, estes dois olham-se com o que resta dos olhos deles e cancelam o ataque com um grunhido de desculpa.
A sua tarefa é, dado um tabuleiro preenchido com uma configuração inicial encontrar a configuração final. Haverá sobreviventes?
Um exemplo de configuração inicial pode ser:

neste caso a configuração final é:

Tarefa por realizar:
Defina a função zombie_attack : char array array -> char array array que recebe a configuração inicial na forma de uma matriz quadrada de caracteres, e que calcula e devolve a configuração final.
Os caracteres que compõem a matriz são alternativamente a caracter * ("asterisco", que representa uma célula que alberga um zombie), ou a caracter X (que representa uma célula que contém um corajoso gato), ou finalmente a caracter . (“ponto”, que representa uma célula que contém um inocente transeunte).
A matriz não terá tamanho maior do que 1000.
Exemplos de entrada
xxxxxxxxxx71*...*..2..XX...3.X..X..4..X..X.5X.X.X..6.X.X...7X.....*
Exemplo de saída
xxxxxxxxxx71*******2**XX***3*X..X**4**X..X*5X*X.X**6.X*X***7X******
Ex. Maioria absoluta!
Imagine um processo eleitoral que os candidatos são designados por um identificador inteiro (1,2,3 etc..).
Um voto, nesta configuração, é um inteiro que representa o candidato escolhido pelo votante. Por exemplo o voto , para designar que se votou no candidato .
Os votos são recolhidos num vetor e pretendemos então saber se existe maioria absoluta numa determinada votação. Neste caso o candidato com a maioria dos votos é vitorioso.
- Define a função
maioria : int array -> intque devolve o identificador do candidato vitorioso caso este tenha a maioria dos votos. Caso não haja maioria absoluta, a exceçãoNot_foundé lançada. - Analise o comportamento da solução proposta. Assuma que a eleição tem candidatos e que se recolheu votos. No pior caso, quantas células do vetor teve de comparar para calcular a resposta? Qual é o tamanho da informação suplementar que teve de declarar para poder calcular a resposta (quantas variáveis auxiliares, quantos vetores auxiliares e de que tamanho)?
Existe um algoritmo, designado de Algoritmo MJRTY da autoria de R. Boyer e J. Moore, definido em 1980 e que permite determinar se há vencedor por maioria no máximo em comparações e que precisa de somente de variáveis para além do vetor dos votos. Outra vantagem é este não precisar de conhecer com quantos candidatos a votação conta.
A referência é
Robert S. Boyer, J. Strother Moore. MJRTY - A Fast Majority Vote Algorithm. In R.S. Boyer (ed.), Automated Reasoning: Essays in Honor of Woody Bledsoe, Automated Reasoning Series, Kluwer Academic Publishers, Dordrecht, The Netherlands, 1991, pp. 105-117. http://www.cs.utexas.edu/users/boyer/mjrty.ps.Z
O algoritmo é
x1Prelúdio: Os candidatos são designados por inteiros.2 a é o vetor dos votos 34seja m uma variável inteira e i um contador inicializado a 056para cada elemento x de a7 se i = 0 então m:=x e i:=18 senão se m = x então incrementar i9 senão decrementar i1011se i=0 então lançar Not_found12se i > ⌊|a|/2⌋ então retornar m1314reinicializar i para 015para cada elemento x de a16 se x = m então incrementar i17 18se i > ⌊|a|/2⌋ então retornar m19senão lançar Not_foundO primeiro ciclo do algoritmo pode ser graficamente apresentado da seguinte forma:
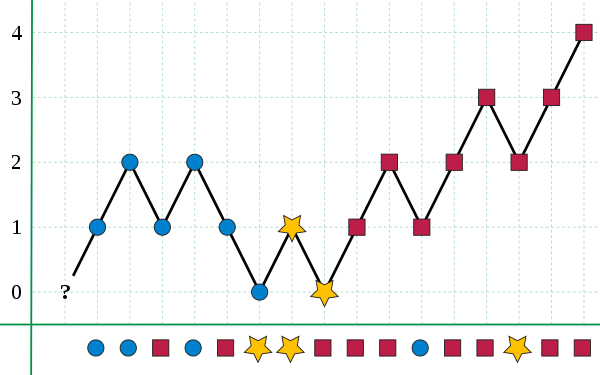
(retirado da wikipedia)
e serve para propor um candidato vencedor. Sabe-se que será com certeza vitorioso por maioria absoluta se a vantagem que tem pelo valor de for de facto maior do que metade dos votos. Sabemos que a votação não discriminou nenhum vencedor se este mesmo valor for 0. Em qualquer outro caso, não se consegue apurar nada. Precisamos de uma nova contagem esclarecedora, desta vez dos votos do candidato proposto à vitória.
No exemplo da imagem, se a votação só tivesse os 7 primeiros votos, então o candidato amarelo teria sido desmentido como vencedor no segundo ciclo.
Implemente a função
mjrty :int list -> intque implementa este algoritmo.Por exemplo
mjrty [1; 1; 2; 1; 2; 3; 3; 2; 2; 2; 1; 2; 2; 3; 2; 2] = 2No caso de não haver vencedor por maioria absoluta, a função deverá lançar a exceção
Not_found.
Ex. O problema da bandeira holandesa.
Este problema de programação foi originalmente proposto pelo Edsger Dijkstra para ilustrar e evidenciar algumas propriedades esperadas de um algoritmo de ordenação, como a estabilidade.
Dada uma sequência arbitrária de bolas de 3 cores de comprimento também arbitrário. Como ordenar esta sequência por forma a que a sequência fique ordenada (as bolas azuis primeiro, seguido das bolsas brancas e finalmente as bolas vermelhas)? Mais, pretende-se que a ordem original das bolsas de mesma cor seja respeitada !
Por exemplo, na sequência por ordenar , se uma bola azul particular está numa posição mais a esquerda de que uma outra bola de cor azul, então na sequência ordenada esta ordem se mantém (continua numa posição mais a esquerda do que a outra). Diz-se desta ordenação que é estável.
O algoritmo proposto por Dijkstra para este problema mostra que é possível ordenar uma coleção de objetos coloridos usando um número linear de comparações de cores, embora os algoritmos de ordenação clássica (a família dos algoritmos de ordenação que não usa a informação particular sobre os objetos por ordenar, por exemplo aqui o conhecimento de que só há três cores, azul, branco e vermelho) precisam em média (e no pior caso nos melhores algoritmos) de um número maior de comparações, na ordem de .
Vamos assumir o tipo OCaml para representar as cores e as funções utilitárias seguintes:
xxxxxxxxxx41type color = Blue | White | Red2type bola = (color*int)3let cor (c,_):bola = c 4let indice (_,i):bola = i
Propomos então um pseudocódigo para a ordenação desejada. Tenha em atenção que este pseudocódigo tem propositadamente erros "subtis" !
xxxxxxxxxx161entreada: a: um vetor de elementos de tipo bola23b := 04i := 05r := comprimento de a67Enquanto i < r fazer8 se cor a[i] = Blue então 9 trocar os valores de a[b] e a[i]10 incrementar b 11 senão se cor a[i] = White então 12 incrementar i13 senão // cor a[i] = Red14 incrementar r15 trocar os valores de a[r] e a[i]16 fim fazer
Após executar este pseudocódigo no papel e corrigido os erros que este contém, defina a função
dutch_flag : bola array -> bola arrayque ordena o vetor parâmetro usando este algoritmo. Com o parcolor * intassociamos um índice a cada cor, o que permitirá verificar facilmente que o algoritmo proposto é estável.Assim
dutch_flag [(Red,0);(White,1);(Blue,2);(Red,3);(Blue,4);(White,5);(Blue,6);(Red,7);(White,8);(Blue,9)] = [(Blue,2);(Blue,4);(Blue,6);(Blue,9);(White,1);(White,5);(White,8);(Red,0);(Red,3);(Red,7)]
Ex. Códigos de Gray.
Os códigos de Gray permitam uma codificação binária cómoda em que um só bit difere entre elementos consecutivos.
Para simplificar, iremos nos restringir ao caso dos inteiros. Neste caso, a codificação de é e a codificação de é . A codificação de é , a codificação de 18 é e a codificação de é .
Uma forma simples de gerar os códigos de gray dos valores inteiros até ao tamanho (por exemplo tem uma codificação de tamanho ) é designada de método reflex-and-prefix.
Este método pode ser ilustrado pela figura seguinte.
xxxxxxxxxx181Base espelho/prefixo n.1 espelho/prefixo n.2 espelho/prefixo n.3 20 0 0 *0 0 00 0 *00 0 000 0 *000 0 000031 1 1 *1 1 01 1 *01 1 001 1 *001 1 0001 4 espelho prefixo 2 *11 2 011 2 *011 2 00115 2 *1 2 11 3 *10 3 010 3 *010 3 00106 3 *0 3 10 espelho prefixo 4 *110 4 01107 4 *10 4 110 5 *111 5 01118 5 *11 5 111 6 *101 6 01019 6 *01 6 101 7 *100 7 010010 7 *00 7 100 espelho prefixo11 8 *100 8 110012 9 *101 9 110113 10 *111 10 111114 11 *110 11 111015 12 *010 12 1010 16 13 *011 13 101117 14 *001 14 1001 18 15 *000 15 1000
Define uma função
gray_list int -> string listque dado um calcula todos os códigos de gray de tamanho . Estes código são devolvidos na forma de uma lista de strings.Caso o argumento seja inválido, a exceção
Invalid_argument "gray_list"é lançada.Por exemplo
gray_list 2 = ["000";"001";"011";"010";"110";"111";"101";"100"]Define uma função
gray_code : int -> stringque dê o código de gray de um determinado inteiro em parâmetro, na forma de uma string.
O método reflex-and-prefix é de implementação simples mas não é eficiente. É possível calcular as codificações e descodificações de forma direta.
O algoritmo de codificação de um número b num código de Gray g é muito simples, se usarmos operadores bitwise:
xxxxxxxxxx11g = b ^ (b >> 1)
Descodificação rápida para palavras de 64 bits (para 32, basta substituir o valor 32 por 16 no código) em C:
xxxxxxxxxx121long grayInverse(long n) {2 long ish, ans, idiv;3 ish = 1;4 ans = n;5 while(1) {6 idiv = ans >> ish;7 ans ^= idiv;8 if (idiv <= 1 || ish == 32) // trocar 32 por 16 no caso duma representação 32 bits9 return ans;10 ish <<= 1; // duplica o número de shifts da próxima vez11 }12 }Define uma função
gray : int -> intque calcula a codificação gray do seu parâmetro inteiro positivo.Caso o argumento seja inválido, a exceção
Invalid_argument "gray"é lançada.Por exemplo
gray 9 = 13(13 = 1101 em binário).Define a função
de_gray : int -> intque faz a operação inversa, o da descodificação.Caso o argumento seja inválido, a exceção
Invalid_argument "de_gray"é lançada.Assim,
de_gray 13 = de_gray 0b1101 = 9(0b1101é 13 em notação binária ).
Ex. Problema da sublista máxima.
O problema da sublista máxima consiste em encontrar numa lista de inteiros positivos ou negativos a maior soma dos elementos de uma sublista (contíguos) da lista dada.
Por exemplo, na lista [ -3, 6, -3, 4, -1, 2, 2, -5, 4 ], a sublista de maior soma é [4, -1, 2, 2] cuja soma é 7. Esta lista pode não ser única. Assim [ -3, 7, -3, 4, -1, 2, 2, -5, 4 ] tem duas sublistas de soma máxima 7. Mas a maior soma, sim.
Para resolver este problema de forma eficaz Jay Kadane (Carnegie Mellon University) propôs em 1984 um algoritmo que resolve este problema percorrendo uma só vez a lista.
O algoritmo é descrito recursivamente da forma seguinte :
- se a lista l é vazia, então a soma máxima é
- se a lista l é da forma e é a maior soma possível para a sublista que termina em , então a maior soma de é .
- Defina uma função
max_kadane : int list -> intque implementa o algoritmo de Kadane acima descritas e que assim devolve o valor da maior soma possível para uma sublista contígua da lista em parâmetro. Poderá usar, se necessário, uma lista auxiliar para memorizar as maiores somas previamente calculados. - Escreva uma função
kadane : int list -> int listque devolve a lista ( localizada o mais a esquerda, no caso de não ser a única) de soma máxima.
Nível Consolidado
Ex. subsequência de listas.
Defina uma função subseq : a list -> 'a list -> bool que determina se uma lista w1 é uma subsequência de uma outra lista w2. Por w1 subsequência de w2 entendemos que podemos obter w1 de w2 removendo ou mais elementos desta última. Por exemplo [4;7;5;1] é uma subsequência de [4;5;4;6;2;7;5;6;8;1;0]. De notar que este processo é um processo importante na analise computacional do genoma.
Ex. Parentesar bem.
Ter um texto bem parentesado, isto é com os símbolos "(" ")" devidamente usados, é uma necessidade comum, e de particular importância quando estes textos são alvo de um processamento por computador (pense num compilador, por exemplo).
Vamos neste exercício propor a verificação do bom uso de parêntesis em qualquer texto organizado na forma de uma lista de caracteres.
Um texto é bem parentesado se a qualquer ocorrência de "("
- está associada uma ocorrência de ")" à sua direita
- que o texto entre estes "(" ")" está também bem parentesado.
Tenha em atenção que, em consequência, a concatenação de dois textos bem parentesados dá um texto bem parentesado, e que colocar um texto bem parentesado entre parêntesis dá um texto bem parentesado.
Defina uma função
verificar : char list -> char list -> boolque verifica se o texto contido no primeiro parâmetro está bem parentesado. Sugere-se o uso do segundo parâmetro (outrachar list, que designaremos de acumulador) para acumular os resultados intermédios da verificação. Assim, no início da verificação o acumulador está vazio, e se no decorrer da verificação o acumulador tiver como primeiro elemento uma parêntesis "(", então a situação atual da verificação ainda aguarda por um parêntesis ")" que corresponde ao fecho do parêntesis do acumulador. Um uso adequado deste acumulador facilita em muito a verificação !Por exemplo :
verificar ['a';'(';'a';'b';'(';'b';')';'c';'(';'o';'k';'a';')';'n';')';'h'] [] = true
Ex. A transformada de Burrows-Wheeler.
A transformada de Burrows-Wheeler (BWT) é um processo de pré-tratamento para a compressão de dados, inventado por Michael Burrows e David Wheeler em 1984 (apos primeiros resultados de D. Wheeler) . Não se trata de um algoritmo de compressão visto este não reduzir o tamanho do texto processado mas a BWT tem a propriedade de calcular permutações do texto que agrupam caracteres semelhantes. Estes agrupamentos fazem do texto resultante um candidato particularmente interessante para métodos de tipo RLE (ver exercício desta ficha).
É uma técnica usada em sistemas de compressão como o bzip2 ou ainda na área da genómica computacional onde encontra aplicações na procura de alinhamento de sequências ou de repetições.
Mais detalhe em:
- Michael Burrows, D. J. Wheeler: "A block-sorting lossless data compression algorithm", 10th May 1994, Digital SRC Research Report 124.
- Artigo do Dr. Dobb's sobre Burrows-Wheeler
O objetivo deste exercício é implementar o processo de codificação e o processo de descodificação. Para tal vamos ilustrar o processo com um exemplo completo para cada um dos processos.
Pretendemos codificar com BWT a palavra "ANAGRAMA"
Codificação:
Primeiro, criamos uma matriz de characteres quadrada do tamanho da palavra por codificar. Esta matriz é preenchida fazendo um shift rotativo a direita:
xxxxxxxxxx101 matriz 23A N A G R A M A4A A N A G R A M5M A A N A G R A6A M A A N A G R 7R A M A A N A G8G R A M A A N A9A G R A M A A N10N A G R A M A AOrdena-se as linhas desta matriz por ordem alfabética
xxxxxxxxxx101 matriz # linha 23A A N A G R A M 14A G R A M A A N 25A M A A N A G R 3 6A N A G R A M A 47G R A M A A N A 58M A A N A G R A 69N A G R A M A A 710R A M A A N A G 8
A codificação será então o par (4,"MNRAAAG"). O 4 é o número da linha onde está a palavra original na matriz ordenada. A palavra "MNRAAAG" é a palavra constituída das letras da ultima coluna, de cima para baixo.
A decodificação começa em (4,"MNRAAAG") e reencontra apalavra "ANAGRAMA" sem o conhecimento, claro, desta matriz.
Escreva uma função
bwt: string -> int*stringque codifica uma palavra com o método BWT.Assim
bwt "anagrama" = (4,"mnraaag").Escreva uma função
debwt : int * string -> string. Por exemplo,debwt (4,"mnraaag") = "anagrama".
Ex. Crise de petróleo.
O Sr. Smith está apaixonado e planeia visitar a dona de seu coração, Sra. Wesson. Mas também é avarento, o combustível é caro e a viagem tem que ser a mais barata possível, porque, como diz ao amigo Beretta, "dinheiro é para pão e rosas, não para combustível". Portanto, ele tem que planear com muito cuidado em quais estações de serviço ele deve parar e abastecer e quanto abastecer.
O seu objetivo é ajudá-lo a planear a rota mais barata.
Por causa de sua avareza, o Sr. Smith acredita que tem que conduzir muito suavemente para obter o menor consumo (litros de combustível por 100 quilómetros). De facto, nas suas viagens de carro, obtém um consumo constante, digamos litros de gás por 100 quilômetros. Considere que a capacidade do tanque de combustível do Sr. Smith é de litros.
A Sra. Wesson vive a quilômetros do Sr. Smith e existem postos de gasolina ao longo do caminho. Estes são ordenados da estação à estação . Suponha, por uma questão de simplicidade, que seja menor ou igual a . Para um posto de gasolina, digamos , o preço do combustível por litro é , e a distância até o próximo posto de gasolina é . Suponha que para todos os e tais que , implica que (todos os s são distintos) . A distância entre o último posto de gasolina e a casa da Sra. Wesson é . Admita que para todos , tais que é maior que . Temos então .
Suponha que o tanque do carro do Sr. Smith esteja vazio no início da viagem e que esteja estacionado ao lado do primeiro desses postos. O posto é o ponto de partida. Suponha que todos os preços sejam distintos (não há dois postos de gasolina oferecendo o mesmo preço).
Numa imagem, a situação é a seguinte:
xxxxxxxxxx51Mr. Smith Mr. Smith's heart2Station 0 Station 1 Station 2 ... Station n-1 |3 *----------------*---------------*----------...----------*------------------*4 <------d0------> <-----d1------> <--d2---- ... -d(n-2)-> <-----d(n-1)----->5 <---------------------------------- d -----... --------------------------->Seu trabalho é estabelecer em que postos de combustível ele tem de parar e quantos litros de combustível ele tem de abastecer em cada um deles para fazer a viagem mais conta possível. Lembre-se de que, em tal situação, o carro do Sr. Smith chega à casa da Sra. Wesson com o tanque vazio.
Para tal, escreva a função val percurso : (c:float) -> (l:int) -> (n:int) -> (dists: int array) -> (prices: float array) -> (int*float) list onde:
cé o consumo (litros por 100 km) conseguido pelo Sr. Smith;lé a capacidade do depósito de combustível do carro do Sr. Smith;né o número de estações de serviço a considerar no percursodistsé o vetor das distâncias entre cada estação de serviço (os s)pricesé o vetor dos preços praticados para o combustível em cada estação (os s)
O retorno da função é a lista ordenada pelo identificador numérico dos postos de gasolina onde o Sr. Smith tem de parar e para cada posto a quantidade de gasolina teve de atestar (na forma de um flutuante, com precisão de duas décimas). Se não é possível realizar tal percurso, a lista devolvida é vazia.
Por exemplo, com a entrada
xxxxxxxxxx51c = 7.82l = 303n = 54dists = [|170;100;150;120;50|]5prices = [|0.49;0.42;0.52;0.53;0.57|]
o resultado de percurso c l n dists prices deverá ser:
xxxxxxxxxx11[(0,13.26);(1,30.00);(2,2.76)]
Com a entrada
xxxxxxxxxx51c = 8.82l = 303n = 34dists = [|250;350;220|]5prices = [|0.50;0.55;0.45|]
o resultado é :
xxxxxxxxxx11[]
Ex. Luigi’s Pizzeria - From MIUP 2018.
Luigi’s new pizzeria has been the talk of the town in the past few weeks. Not only because it has the best pizzas you can find for miles, but also because of its crazy all you can eat policy.
You see, Luigi’s pizzas are enormous, and they are cut into very thin slices. And that’s not even the crazy part! Each slice has different ingredients and you can eat as many slices as you want. But there is one small caveat. You can only select adjacent slices and you have to eat them all! It is therefore very tricky for each client to select the best part of the pizza according to his own taste.
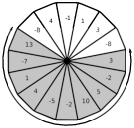
Figure 1: Selected slices must be adjacent. The section in grey has a score of 20.
You enter the restaurant and see that today’s special pizza has been cut into N slices. After attributing scores to each one of the slices, you must devise an algorithm that selects the section of the pizza that yields the best value according to those scores. The value of a section of pizza is the sum of the scores of its slices. Notice that slice scores can be negative.
- Define a function
score :int -> int list -> intthat takes the number of slices in the pizza and a list of integer ne contains the integers () that represent the score you attributed to each slice. These values follow these constraints :
| Number of slices. | |
|---|---|
| Value of each slice. |
The function returns an integer that is equal to the value of the best possible section of adjacent pizza slices. The smallest possible section would be a single slice.
For instance,
score 4 [2;-2;3;-1]returns4.score 16 [-1;1;3;-8;3;-2;5;10;-2;-5;4;1;-7;13;-8;4]returns20.score 4 [-1;-2;-3;-4]returns-1.