 Apresentamos aqui outro teste com uma expressão regular que especifica
as palavras com um número par de ocorrências da letra b :
Apresentamos aqui outro teste com uma expressão regular que especifica
as palavras com um número par de ocorrências da letra b :
A ideia de partida é a seguinte: se um autómato finito reconhece a expressão regular r, então para toda a letra de uma palavra reconhecida podemos lhe fazer corresponder uma letra contida em r. Para distinguir as diferentes occorências de uma mesma letra em r, vamos indexá-los com inteiros. consideremos por exemplo a expressão regular (a|b)* a (a|b), que define as palavras sobre o alfabeto {a,b} cuja penúltima letra é um a. Se indexamos os caracteres, obtemos
(a1|b1)* a2 (a3|b2)
a1a1b1a1a2b2
A ideia é, então, de construir um autómato cujos estados são conjuntos de letras indexadas, correspondendo às occorências que podem ser lidas num dado momento. Desta forma, o estado inicial contem as primeiras letras possíveis das palavras reconhecidas. No nosso exemplo, estas são a1,b1,a2. Para construir as transições, basta calcular, para cada ocorrência de uma letra, o conjunto das ocorrências que podem estar em seguida. No nosso exemplo, se acabamos de ler a1, então os caracteres possíveis seguintes são a1,b1,a2 ; se acabamos de ler a2, então estes são a3,b2.
type ichar = char * int type regexp = | Epsilon | Character of ichar | Union of regexp * regexp | Concat of regexp * regexp | Star of regexpDefinir uma função
val null : regexp -> boolque determina se epsilon (a palavra vazia) pertence à linguagem reconhecida pela expressão regular dada um parâmetro.
module Cset = Set.Make(struct type t = ichar let compare = compare end)
Definir uma função
val first : regexp -> Cset.tque calcula o conjunto das primeiras letras das palavras reconhecidas por uma expressão regular. (Esta deverá usar a bom proveito a função null.)
De forma semelhante, definir uma função
val last : regexp -> Cset.tque calcula o conjunto das últimas letras das palavras reconhecidas.
val follow : ichar -> regexp -> Cset.tque calcula o conjunto das letras que podem ocorrer a seguir a uma dada letra dentro do conjunto das palavras reconhecidas.
De notar que a letra d pertence ao conjunto follow c r se e só se
Definir uma função
val next_state : regexp -> Cset.t -> char -> Cset.tque calcula o estado que resulta de uma transição.
Para representar o autómato finito dá-mo-nos o tipo OCaml seguinte :
module Cmap = Map.Make(Char)
module Smap = Map.Make(Cset)
type state = Cset.t
type autom = {
start : state;
trans : state Cmap.t Smap.t
}
Podemos escolher representar o caracter # da forma seguinte :
let eof = ('#', -1)
Definit uma função
val make_dfa : regexp -> automque constrói o autómato correspondente a uma dada expressão regular. A ideia é construir os estados quando necessário, partindo do estado inicial. Poderemos por exemplo escolher a abordagem seguintes :
let make_dfa r =
let r = Concat (r, Character eof) in
(* transições em curso de construção *)
let trans = ref Smap.empty in
let rec transitions q =
(* a função transitions constrói todas as transições do estado q,
se é a primeira vez que este é explorado *)
...
in
let q0 = first r in
transitions q0;
{ start = q0; trans = !trans }
Nota : é, claro, possível construir um autómato cujos estados não são conjuntos mas sim, por exemplo, inteiros, para mais eficiência na execução do autómato. Isto pode, alias, ser feito durante a própria construção, ou a posteriori. Mas isso não é o nosso propósito principal aqui.
let fprint_state fmt q =
Cset.iter (fun (c,i) ->
if c = '#' then Format.fprintf fmt "# " else Format.fprintf fmt "%c%i " c i) q
let fprint_transition fmt q c q' =
Format.fprintf fmt "\"%a\" -> \"%a\" [label=\"%c\"];@\n"
fprint_state q
fprint_state q'
c
let fprint_autom fmt a =
Format.fprintf fmt "digraph A {@\n";
Format.fprintf fmt " @[\"%a\" [ shape = \"rect\"];@\n" fprint_state a.start;
Smap.iter
(fun q t -> Cmap.iter (fun c q' -> fprint_transition fmt q c q') t)
a.trans;
Format.fprintf fmt "@]@\n}@."
let save_autom file a =
let ch = open_out file in
Format.fprintf (Format.formatter_of_out_channel ch) "%a" fprint_autom a;
close_out ch
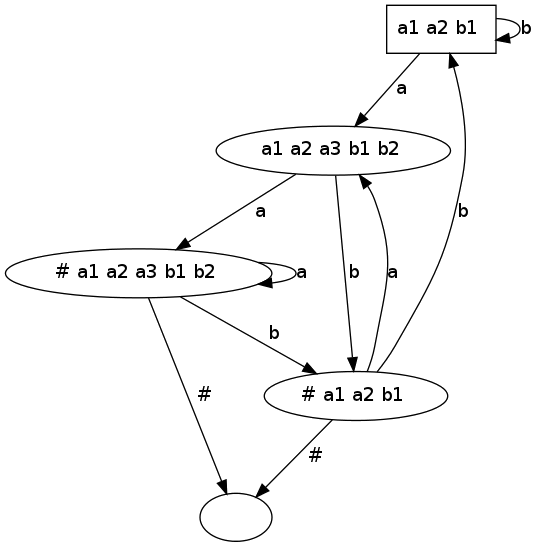 Para testar, retomemos o exemplo préviamente introduzido :
Para testar, retomemos o exemplo préviamente introduzido :
(* (a|b)*a(a|b) *)
let r = Concat (Star (Union (Character ('a', 1), Character ('b', 1))),
Concat (Character ('a', 2),
Union (Character ('a', 3), Character ('b', 2))))
let a = make_dfa r
let () = save_autom "autom.dot" a
A execução produz um ficheiro autom.dot que pode ser visualizado em Unix com o comando
dotty autom.dotou ainda com o comando
dot -Tps autom.dot | gv -Obtém-se algo como a figura à direita.
val recognize : autom -> string -> boolque decide se uma dada palavra é reconhecida por um dado autómato.
Aqui encontram-se alguns testes positivos :
let () = assert (recognize a "aa") let () = assert (recognize a "ab") let () = assert (recognize a "abababaab") let () = assert (recognize a "babababab") let () = assert (recognize a (String.make 1000 'b' ^ "ab"))e alguns testes negativos :
let () = assert (not (recognize a "")) let () = assert (not (recognize a "a")) let () = assert (not (recognize a "b")) let () = assert (not (recognize a "ba")) let () = assert (not (recognize a "aba")) let () = assert (not (recognize a "abababaaba"))
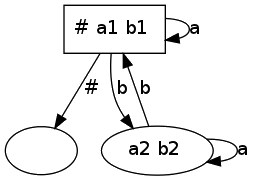
 Apresentamos aqui outro teste com uma expressão regular que especifica
as palavras com um número par de ocorrências da letra b :
Apresentamos aqui outro teste com uma expressão regular que especifica
as palavras com um número par de ocorrências da letra b :
let r = Star (Union (Star (Character ('a', 1)),
Concat (Character ('b', 1),
Concat (Star (Character ('a',2)),
Character ('b', 2)))))
let a = make_dfa r
let () = save_autom "autom2.dot" a
Alguns testes positivos :
let () = assert (recognize a "") let () = assert (recognize a "bb") let () = assert (recognize a "aaa") let () = assert (recognize a "aaabbaaababaaa") let () = assert (recognize a "bbbbbbbbbbbbbb") let () = assert (recognize a "bbbbabbbbabbbabbb")e alguns testes negativos :
let () = assert (not (recognize a "b")) let () = assert (not (recognize a "ba")) let () = assert (not (recognize a "ab")) let () = assert (not (recognize a "aaabbaaaaabaaa")) let () = assert (not (recognize a "bbbbbbbbbbbbb")) let () = assert (not (recognize a "bbbbabbbbabbbabbbb"))
Mais precisamente, vamos produzir código da forma seguinte :
type buffer = { text: string; mutable current: int; mutable last: int }
let next_char b =
if b.current = String.length b.text then raise End_of_file;
let c = b.text.[b.current] in
b.current <- b.current + 1;
c
let rec state1 b =
...
and state2 b =
...
and state3 b =
...
O tipo buffer contém a string por analisar
(campo text), a posição do próximo caractere por examinar
(campo current) e a posição que segue o último lexema
reconhecido (campo last). A função next_char devolve
o próximo caracter por analisar e incrementa o campo
current. Se se atinge o final de string, esta função levanta
a excepção End_of_file.
A cada estado do autómato corresponde uma função statei com um argumento b de tipo buffer. Esta função executa a tarefa seguinte :
Definir uma função
val generate: string -> autom -> unitque toma em argumento o nome de um ficheiro e um autómato e que produz em saída (no ficheiro em causa) o código OCaml que corresponde ao referido autómato, conforme o formato descrito anteriormente. Indicação :
let start = state42correspondendo ao estado inicial do autómato (aqui state42, para efeito de ilustração).
Para testar, escrever (num outro ficheiro lexer.ml, desta vez escrito à mão) um programa que corta uma string em lexemas, usando o código produzido automaticamente (atribuindo de forma fixa o nome do ficheiro, por exemplo a.ml). O princípio por seguir descreve-se com base num ciclo que efectua as ações seguintes :
O programa resultante poderá ser testar, por exemplo, com a expressão regular a*b, executando
let r3 = Concat (Star (Character ('a', 1)), Character ('b', 1))
let a = make_dfa r3
let () = generate "a.ml" a
e depois ligando o código produzido com o ficheiro lexer.ml :
% ocamlopt a.ml lexer.mlAtuando sobre a string abbaaab, a análise deve produzir três lexemas e terminar com sucesso :
--> "ab" --> "b" --> "aaab"Atuando sobre a string aba, a análise deve produzir um primeiro lexema e depois terminar com fracasso :
--> "ab" exception End_of_fileEnfim, tendo em conta a string aac, a análise deve falhar com um erro lexical :
exception Failure("lexical error")
Pode-se igualmente testar o programa com a expressão regular
(b|espilon)(ab)*(a|epsilon) que codifica as palavras que
alternam as letras a e b.
Sobre a string abbac, o programa deverá resultar nos três
lexemas seguintes :
--> "ab" --> "ba" --> "" would now loopSendo o último lexema a string vazia, o programa para, acrescentando que se obtém agora infinitamente o lexema vazio.