Ficha OCaml : Tipos soma

Exercício : Digressões sobre árvores binárias

Neste exercício vamos redescobrir uma estrutura de dados clássica, as árvores binárias, mas com um pequeno twist. Queremos guardar a altura de uma árvore no nodo raiz da árvore. Tal situação é relevante se o uso que temos das árvores nos obriga recorrentemente ao uso desta informação. Calcular a altura de uma árvore é custoso! Compensa assim trocar memoria por computação e arquivar esta informação na própria árvore. Uma preocupação que teremos ao manipular tais árvores é a gestão da altura. Quem trata do adequado arquivo? será razoável pedir este tratamento ao utilizador destas árvores?¹ Não será melhor atribuir esta tarefa às funções da biblioteca que fornece esta estrutura de dados? Temos então aqui um campo de uma estrutura de dados que deve responder a uma propriedade (ser de facto a altura da árvore em causa, em qualquer momento da sua existência) e cuja manipulação convém ser ocultada ao utilizador da biblioteca.

Vamos também considerar que as árvores em questão possam ser árvores vazias. Veremos que esta escolha nos obriga a alguns cuidados quando pretendemos determinar a altura de uma árvore. Como representamos uma folha? Qual é a altura de uma árvore quando esta é vazia, ou então quando esta é uma folha?

1. Define o tipo (polimórfico) 'a abin das árvores binárias eventualmente vazias com a informação da altura em cada nodo (por exemplo uma árvore de altura x tem esta informação arquivada na raiz);
2. define as funções empty : unit -> 'a abin e node : a abin -> 'a -> 'a abin -> 'a abin' tal que empty () crie uma árvore vazia e node esq x dir crie uma árvore cuja raiz contém x e que tenha por filho esquerdo a árvore esq e por filho direito a árvore dir, com a informação adequada para a altura arquivada no nodo raiz. Tais funções são designadas de smart constructors por construírem elementos de um tipo de dado tratando da logística própria do tipo para a qual não queremos o envolvimento do utilizador, aqui o arquivo correto da altura da árvore construída;
3. define a função height : 'a abin -> int que calcula a altura de uma árvore;
4. define a função leaves : 'a abin -> int que calcule o número de folhas de uma árvore;
5. define a função nodes : 'a abin -> int que calcula o número total de nós de uma árvore, folhas incluídas;
6. define a função duplicate : 'a abin -> bool que devolve true se existe um elemento duplicado na árvore em parâmetro;
7. define a função sorted : ('a -> 'a -> int) -> 'a abin -> bool tal que sorted comp ar que devolve true se a árvore ar for uma árvore binária de pesquisa conforme o critério de comparação comp.
8. define a função fold_dfs f init ar que, a semelhança do fold_left para as listas, aplica uma função binária f a todos os elementos da árvore binária ar usando a estratégia dfs (depth-first-search, em profundidade primeiro, da esquerda para a direita). O valor inicial do acumulador (que acumula o resultado da função f no percurso dfs) é init;
9. define igualmente a função map f ar sobre as árvores binárias;
10. define a função fold_bfs f init ar (breadth-first search, em largura primeiro, da esquerda para a direita) que aplica a função binária f a todos os elementos da árvore ar. O valor inicial do acumulador é init;
11. proponha uma versão recursiva terminal de fold_dfs.

Exercício : Fórmulas lógicas proposicionais

O objetivo deste exercício é a exploração dos tipos soma. No caso deste exercício estamos interessado no tipo das expressões lógicas (proposicionais). Considere a fórmula proposicional seguinte:

Essa fórmula pode ser comodamente representada na forma de uma árvore (designada comumente de termo)

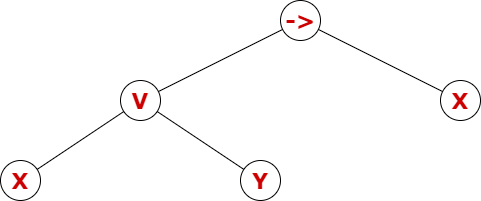
1. Define o tipo prop das expressões lógicas proposicionais que envolvem variáveis proposicionais, os valores $\top$, $\bot$, a negação , a implicação, a disjunção, a conjunção e a equivalência. Este tipo codifica uma fórmula proposicional como um termo.

   Neste exercício assume-se que as variáveis proposicionais são de tipo string;

2. define a função valor : (string*bool) list -> prop -> bool que dado uma lista associativa das variáveis para os seus valores de verdade, devolve o valor de verdade da fórmula. Por exemplo, valor [("X",true); ("Y",false)] f = true onde f é a representação de tipo prop da fórmula $X \lor Y \to X$;

3. define a função vars : prop -> string list que devolve a lista das variáveis que ocorrem na fórmula em parâmetro. A lista resultante não deverá conter elementos duplicados;

4. define a função tabela_verdade : prop -> bool array array que calcula a tabela de verdade da fórmula em parâmetro. Por exemplo tabela_verdade f , em que f é a representação de tipo prop da fórmula $X \lor Y \to X$, devolve a tabela :

   $$\begin{array}{|l|l|l|}\hline true & true & true \\ \hline true & false & true \\ \hline false & true & true \\ \hline false & false & true \\ \hline \end{array}$$

   que corresponde à tabela de verdade

   $$\begin{array}{|c|c|c|} \hline X & Y & X \lor Y \to X\\ \hline\hline true & true & true \\ \hline true & false & true \\ \hline false & true & true \\ \hline false & false & true \\ \hline \end{array}$$

Exercício : Calcular e derivar

Considere a expressão aritmética seguinte:

Podemos representar esta expressão pela árvore (termo) seguinte :

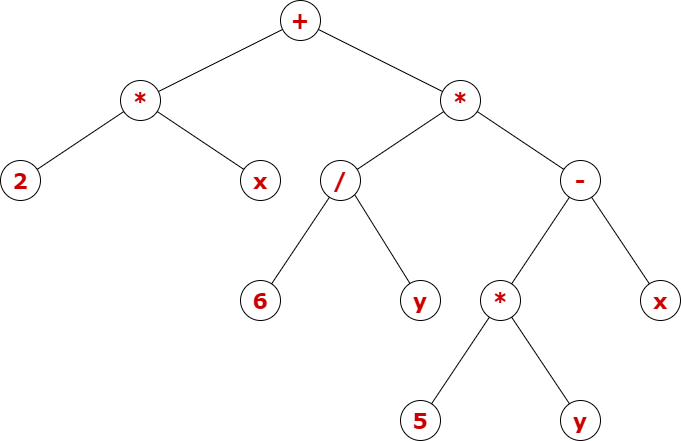
1. Define o tipo exp das expressões aritméticas sobre inteiros e com variáveis (aqui codificadas com o tipo string) envolvendo exclusivamente as operações básicas (soma, substração, produto, divisão);
2. se souber que a variável x tem por valor 2 e y vale 1, então a expressão dada em exemplo vale 22. Define assim a função calcula : (string * int) list -> expr -> int que calcula o valor associado a uma expressão dada em parâmetro com base no valor das suas variáveis, também fornecido como parâmetro. Assim calcula [("x",2);("y",1)] e = 22 onde e é a expressão aritmética dada no exemplo;
3. defina a função deriva : expr -> string -> expr que calcula a derivada de uma expressão numa variável. Assim deriva e x devolve a expressão aritmética que é a derivada de e na variável x.