Ficha OCaml 3. Cálculo e recursividade.
Ficha OCaml 3. Cálculo e recursividade.Nível BásicoEx. Contas simples.Ex. Distância de Manhattan.Ex. Um algoritmo histórico.Ex. a melhor forma de chegar ao infinito e mais além.Ex. Aproximar .Ex. Algarismos.Ex. As sequências de Hofstadter-Huber Qr,s(n).Ex. As sequência fêmeas e machos de Hofstadter. Nível IntermédioEx. Somatórios.Ex. Tribonacci.Ex. recursividade terminal.Ex. Exponenciação rápida.Ex. Catalã: um povo, um creme e uns números.Ex. Dicotomia.Ex. A função 91 de McCarthy.Ex. Contar triângulosEx. A conjectura de Collatz ou de Hailstones ou de Syracuse ou de mais uns nomes giros...Ex. Estrelinhas como fractais textuais.Ex. Números de Bell.Nível ConsolidadoEx. Tribonacci em tempo logarítmico.Ex. Quantas montanhas?Ex. A grandeza do Dragão.Ex. As Torres de Hanói.
Nível Básico
Ex. Contas simples.
- Define uma função
distancia : (float * float) -> (float * float) -> floatque calcula a distancia euclidiana entre dois pontos dados em parâmetros. - Defina uma função
area: float -> floatque calcula a área de um círculo cujo o raio é dado em parâmetro. - Defina uma função
sin2x : float -> floatque, dado um parâmetro flutuante x, calcula a seguinte expressão:
Ex. Distância de Manhattan.
Considere o problema da otimização de rotas de táxi em cidades modernas como Manhattan, por exemplo. Considere o mapa seguinte em que as estradas estão assinaladas a cinzento. Considere igualmente que cada prédio da cidade, os quadrados brancos, tem por dimensão 1 (um).
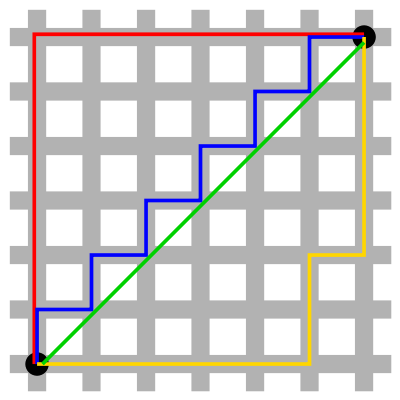
(imagem retirado da wikipédia )
Qual é a menor distância de táxi entre o ponto inferior esquerdo e o ponto superior direito?
Se pudéssemos voar, a distância euclidiana seria a solução (a rota verde). Mas para a distância percorrida de carro, o cálculo deverá ser diferente. Assim sendo, qual é o comprimento da rota a vermelho? da rota azul? ou da rota amarela?
- Com base na resposta a estas questões proponha a implementação em OCaml da função
manhattan_distance : int ->int -> int ->int -> inttal quemanhattan_distance x y z tcalcule a distância de Manhattan entre o ponto e o ponto .
Ex. Um algoritmo histórico.
Vamos implementar neste exercício um algoritmo histórico, foi formulado pelo próprio Euclides 300 AC.
Em particular, interessa-nos a versão recursiva.
Defina uma função
euclides : int -> int -> intque calcula o maior divisor comum com base no algoritmo acima descrito. Assim,euclides 36 45 = 9.No caso de um argumento inválido, a exceção
Invalid_argument "euclides"é lançada.
Ex. a melhor forma de chegar ao infinito e mais além.
Wilhelm Friedrich Ackermann, matemático alemão, contribuiu ao estudo das funções computáveis apresentando uma função com propriedades inéditas: uma função total computável que fugia, na data da sua descoberta, à classificação que se pensava ser a das funções com estas características.
Em parte porque a função... tem um comportamento explosivo!
A função originalmente proposta tinha 3 parâmetros, mas a que ficou registada para a história contempla dois parâmetros e é definida da seguinte forma:
Calcule no papel o resultado de A(4,4).
Se ler esta frase, fique sabendo que A(4,2) tem como resultado um número com mais do que 19 mil dígitos () e que a alínea anterior resulta de uma piada de mau gosto que não se espere, claro, que resolva!
Agora sim: defina a função recursiva ackermann int -> int -> int que calcula esta função.
Por exemplo ackermann 3 4 = 125
Ex. Aproximar .
A formula de Wallis permite uma aproximação de definida nos termos seguintes:
Proponha uma definição recursiva desta aproximação, na forma de uma função que depende de um índice tal que se a fórmula calculada é , se , a fórmula calculada é , etc.
Tendo definido esta função, implemente esta função em OCaml na forma da função
aproximar_pi : int -> floatque recebe o índice e devolve o resultado de .Considere que . No caso de não ser possível calcular ,
aproximar_pilança a exceçãoFailure "aproximar_pi".Um exemplo de execução é:
aproximar_pi 5 = 3.00217595455690622
Ex. Algarismos.
Escreva uma função
algarismos : int -> int -> int*int*intque recebe um inteiro e um algarismo e devolva o numero de vezes que este algarismo aparece em , a soma dos algarismos de e finalmente o número de algarismos de .Por exemplo,
algarismos 1073741823 3 = (2,36,10)
Ex. As sequências de Hofstadter-Huber Qr,s(n).
Sejam e dois inteiros naturais positivos tais que e . Define-se por sequência de Hofstadter-Huber de família a sequência determinada pela fórmula seguinte
em que é um inteiro positivo.
Esta família de valores sofre de irregularidades. Em particular diz-se que morre quando os valores não estão definidos (i.e. quando ou ), ou quando qualquer outra condição estabelecida sobre e não é respeitada.
Define a função
hhq : int -> int -> int -> inttal quehhq r s ncalcule o valor de .No caso de um argumento inválido ou da deteção de qualquer situação anómala, a exceção
Failure "hhq"é lançada. Assim,hhq 1 4 12 = 7.
Ex. As sequência fêmeas e machos de Hofstadter.
Em "Hofstadter, D. R. Gödel, Escher, Bach: An Eternal Golden Braid. New York: Vintage Books, p. 137, 1989.", Hofstadter definiu várias sequências numérias, uma delas é o par de sequencias fêmeas e machos seguintes:
Define a função
hfm : int -> int*intque, para um parâmetro inteiro positivo n devolve o par (f(n),m(n)).No caso de um argumento inválido ou da deteção de qualquer situação anómala, a exceção
Failure "hfm"é lançada.Assim,
hfm 7 = (5,4).
Nível Intermédio
Ex. Somatórios.
Considere a expressão matemática
- Defina a função
sum3 : int -> inttal quesum3 ndevolva o valor . - Dê uma versão recursiva terminal.
- (opcional, se esta matéria for dada) Dê a versão CPS.
Ex. Tribonacci.
Considere a função tribonacci seguinte, sobre inteiros naturais:
- Define a função recursiva em OCaml.
- Define a versão iterativa (com ciclos e referências) em OCaml.
- Dê uma versão recursiva terminal em OCaml.
Ex. recursividade terminal.
Considere a função seguinte:
1let rec h x y = 2 if x > y then 1 3 else if x < y then 2 * x + h (x - 1) (y - 2) 4 else y * h x (y - 1)
- Dê uma definição recursiva terminal desta função.
Ex. Exponenciação rápida.
Este exercício debruça-se sobre a função de exponenciação inteira . A definição natural e direta desta operação sugere multiplicações. Mas uma definição alternativa simples permite realizar o mesmo cálculo minorando o número de multiplicações:
Tal método de exponenciação é , as vezes, designada de exponenciação rápida.
- Proponha uma função recursiva em OCaml que implemente esta definição.
- Qual é a complexidade desta exponenciação (em número de multiplicações realizadas)?
- Dê uma versão recursiva terminal da exponenciação rápida
Ex. Catalã: um povo, um creme e uns números.
Uma famosa sequência de números inteiros conhecida por Números de Catalan (do matemático belga Eugène Charles Catalan, 1814–1894) é definida por:
Esta sequência está envolvida na contagem de variadíssimos fenómenos combinatórios.
Escreva um programa
catalan : in -> intque recebe um inteiro natural e que calcule recursivamente o valor de .No caso de um argumento inválido, a exceção
Invalid_argument "catalan"é lançada.Assim,
catalan 6 = 132.
Ex. Dicotomia.
Seja v um vetor de inteiros ordenado de forma crescente de tamanho n, e x um inteiro.
Vamos definir uma função de pesquisa eficiente que tire proveito da ordenação do vetor.
Considere dois índices i, j do vetor v tal que . Vamos procurar x no vetor v entre os índices i e j, (notação )
Se então se e só se . Senão:
Se então sabemos que não está no segmento do vetor . No melhor caso, está algures no segmento do vetor .
Se então sabemos que não está no segmento do vetor . No melhor caso, está algures no segmento do vetor .
Se então sabemos que está possivelmente no segmento do vetor . O que sabemos com toda a certeza é que x não está nem em nem em . Por isso a procura deve concentrar-se no segmento .
Temos , então, seja o índice "no meio", ou seja o maior inteiro que é menor ou igual à média de i e j.
- Se , encontramos .
- Se , então o segmento do vetor não contém x. Possivelmente estará em
- Se , então o segmento do vetor v não contém x. Possivelmente estará em
Este médio é designado de procura/pesquisa binária ou procura dicotómica
Defina uma função recursiva de pesquisa binária
binsearch_aux : 'a -> 'a array -> int -> int.binsearch_aux x v low highprocure o valorxno vetor ordenadoventre os índiceslowehigh. Esta função devolve o índice onde o valorxse encontra emv(no intervalolow..high) ou então a exceçãoNot_foundem qualquer outra situação.Por exemplo
binsearch_aux 12 [|1;2;5;7;12;16;23;33;78|] 2 6devolve4.Defina uma função
binsearch : 'a -> 'a array -> intque procura um valor x em todo o vetor ordenadov. Esta função devolve o índice onde o valorxse encontra emvou então a exceçãoNot_found. É aconselhado que use a função do ponto anterior.
De notar que esta pesquisa divide o espaço de procura por dois de cada vez que refina a sua pesquisa. Esta característica melhora em muito os tempos de resposta. O pior caso é quando o elemento procurado não está no vetor. Mesmo assim, o número de comparações realizadas pelo algoritmo nunca ultrapassa a ordem de sendo o tamanho do vetor.
Ex. A função 91 de McCarthy.
Nos anos 70, John McCarthy, um dos pais da inteligência artificial, em parceria com o Zohar Manna e Amir Pnueli, procurou definir uma função recursiva que seja um caso de escola para a verificação de programas.
Esta função é a função definida da forma seguinte:
Define a função
mccarthy : int -> intque implemente esta definição recursiva. Por exemplomaccarthy 200 = 190,mccarthy 24 = 91Considere agora a função f91 definida da forma seguinte:
Define uma função recursiva
mccarthy_is_f91 : int -> int -> boolque verifica se, no intervalo inteiro definido pelos dois inteiros parâmetros, as duas funções devolvem o mesmo resultado. por exemplomccarthy_is_f91 70 120 = mccarthy_is_f91 120 70 = true.
Ex. Contar triângulos
Considere a seguinte sequência de triângulos equiláteros:
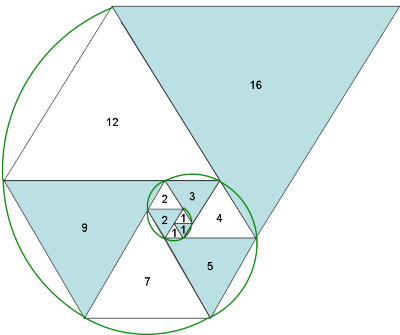
Se listarmos o comprimento dos lados dos triângulos desta sequência temos:
Define uma função
triangulos : int -> intque devolve o n-ésimo elemento desta sequência (que começa no índice 0).Por exemplo
triangulos 0 = 1,triangulos 3 = 2etriangulos 9 = 9
Ex. A conjectura de Collatz ou de Hailstones ou de Syracuse ou de mais uns nomes giros...
A conjetura de Collatz (ou Hailstones, ou de Syracuse) é da autoria do matemático alemão Lothar Collatz que desafiou a comunidade científica durante um evento na Universidade de Syracuse em 1928. A conjetura estabelece uma sequência de números (designada também de trajetória ou voo) que a partir de um número natural inicial obedece aos seguintes critérios:
- se n é par, então o sucessor de n na sequência é n divido por dois;
- se n é impar, então o sucessor de n na sequência é n multiplicado por 3 mais 1.
- juntamos o critério de paragem em 1.
Até a data de hoje, ninguém encontrou um numero inicial, n, que não gere uma trajetória que termine no número ! (sem o critério de paragem, obteríamos um ciclo que passaria ad eternum pelo valor 1)
Exemplos
O seu desafio é escrever a função recursiva
collatz : int -> int listem Ocaml que dado um parâmetro inteiro n, devolva a sequência de inteiros que corresponde a trajetória a partir do valor n. Obviamente esta sequência termina quando se atinge o valor 1. Por exemplocollatz 6 = [6; 3; 10; 5; 16; 8; 4; 2; 1]A função anterior dará rapidamente problemas quando o aumentar. Os valores manipulados aumentam significativamente e pode ser necessário usar uma representação numérica mais abrangente. Para esse problema podemos recorrer ao módulo
zarithque fornece mecanismos de aritmética de precisão arbitrária. O tamanho da trajetória poderá também aumentar de forma significativa. Proponha assim uma função recursivacollatz_big : int -> unitque imprima a trajetória na saída standard. Para esse efeito poderá socorrer-se das seguintes definições:
xxxxxxxxxx91let zero = Z.zero2let one = Z.one3let two = Z.succ one4let three = Z.succ two5let ( +> ) = Z.add (* a soma nos inteiros Z *)6let ( *> ) = Z.mul (* a multiplicação nos inteiros Z *) 7let ( /> ) = Z.div (* a divisão nos inteiros Z *)8let ( %> ) = Z.rem (* o resto da divisão euclidiana nos inteiros Z *) 9(* considere eventualmente as funções : Z.to_string Z.of_string Z.of_int *)Por exemplo, collatz_big 27 devolve a trajetória seguinte no ecrã:
xxxxxxxxxx11212728234141245626317948479142107111214121071332214161154841624217121183641918220912127422137234122420625103263102715528466292333070031350321753352634263357903639537118638593391780408904144542133643668443344516746502472514875449377501132515665228353850544255512765663857319589585947960143861719622158631079643238651619664858672429687288693644701822719117227347313677441027520517661547730777892327946168023088111548257783173284866854338613008765088325899769048891244921229361941849592964697239870993510010610153102160103801044010520106101075108161098110411121121
Ex. Estrelinhas como fractais textuais.
Observe o seguinte padrão constituído de espaços e de asteriscos.
xxxxxxxxxx151*2* * 3 *4* * * *5 *6 * *7 *8* * * * * * * *9 *10 * *11 *12 * * * *13 *14 * *15 *
Descubra as regras de construção que o estrutura e escreva uma função recursiva estrelinhas : int-> unit que dado um parâmetro inteiro , potência de pertencente ao intervalo , reproduza este padrão tal que a maior quantidade em linha de asteriscos seja .
Por exemplo estrelinhas 8 imprime o padrão acima apresentado.
No caso de um argumento inválido, a exceção Invalid_argument "estrelinhas" é lançada.
Ex. Números de Bell.
Quantas formas temos de particionar um conjunto? Por exemplo, quantas formas temos de particionar .
Neste exemplo, temos formas de particionar:
De uma forma geral, designa-se por -ésimo número de Bell, , o número de partição de um conjunto de elementos em sub-conjuntos não vazios.
Uma definição elegante destes números é:
Define uma função
bell : int -> stringque, dado um parâmetro inteiro positivon, calcula .Realça-se que a natureza desta sequência numérica leva a que seja necessária usar um tipo de dados numéricos com precisão arbitrária. OCaml fornece o módulo Zarith, em particular o sub-módulo Z, para esse efeito. Será necessário neste exercício recorrer a ele. Pretende-se que o resultado final seja entregue na forma de uma string contendo o numero calculado (por exemplo recorrendo à função
Z.to_string).Para fins de ilustração,
bell 33 = 1629595892846007606764728147
No caso de um argumento inválido ou da deteção de qualquer situação anómala, a exceção Failure "bell" é lançada.
Nível Consolidado
Ex. Tribonacci em tempo logarítmico.
Recordamos a definição da sequência de tribonacci.
Define a função tribonacci_fast : int -> int que calcula o n-ésimo elemento da sequencia de tribonacci. Assim tribonacci_fast 25 = 1800281, ou tribonacci_fast 42 = 6804250945 instantaneamente.
Para tal aconselha-se que adapte a técnica em uso para calcular a sequência de fibonacci em tempo logarítmico com base na exponenciação rápida de matrizes.
Ex. Quantas montanhas?
Vamos aqui considerar um problema clássico de combinatória (de contagem).
Dada um valor , imagine uma paisagem de montanha inscrita numa grelha até .
No nosso cenário, uma paisagem é constituída exclusivamente de montanhas cujo declive é uma diagonal um por um ascendente ou descendente, que começa em e acaba em .
Não se consideram também perfis de montanha que descem por baixo do eixo dos .
O problema por resolver é: dado (que define o tamanho da paisagem) e o número de picos ( sempre menor ou igual a ), quantos perfis montanhosos válidos existem?
Por exemplo para e , a resposta é . Graficamente podemos visualizar as soluções da seguinte forma:
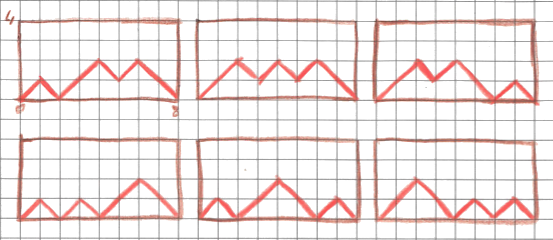
Damos igualmente dois valores limites para , que são e

Assumimos igualmente que e .
- Define uma função
montanhas int -> int -> int optionque calcula precisamente o número de perfis possíveis. Assim o resultado demontanhas 4 3éSome 6. Quando as regras sobre one oknão são cumpridas, ou por uma razão qualquer não é possível calcular o valor, a função montanhas devolveNone. Assim, o resultadomontanha 3 4éNone.
Dica: considere os casos iniciais ( e , seguido de e ou , etc. ) e veja se um padrão emerge a medida que calcula os casos seguintes.
Ex. A grandeza do Dragão.
Imagine a seguinte situação.
Tem uma fita de papel que vai querer dobrar ao meio n vezes.
A configuração inicial é (papel sem dobras, vista de perfil):

Se dobrar uma vez e desdobar e deixar que o angulo faça 90º obtém, de perfil a seguinte figura:

Se dobrar duas vezes e desdobar e deixar que os ângulos obtidos façam 90º obtém, de perfil a seguinte figura:

Se dobrar três vezes e desdobar e deixar que os ângulos obtidos façam 90º obtém, de perfil a seguinte figura:

Muito rapidamente o exercício de dobra de papel torna-se penoso mas visualmente interessante (retirado do Wikipédia):
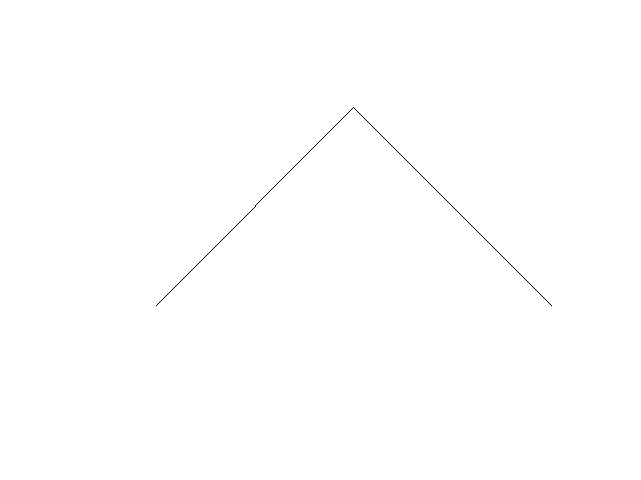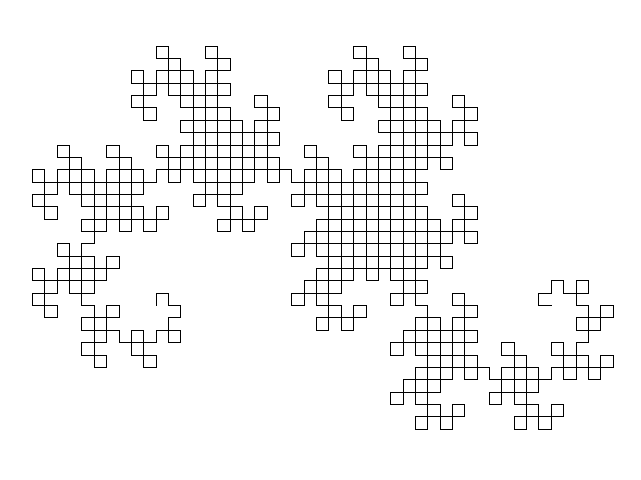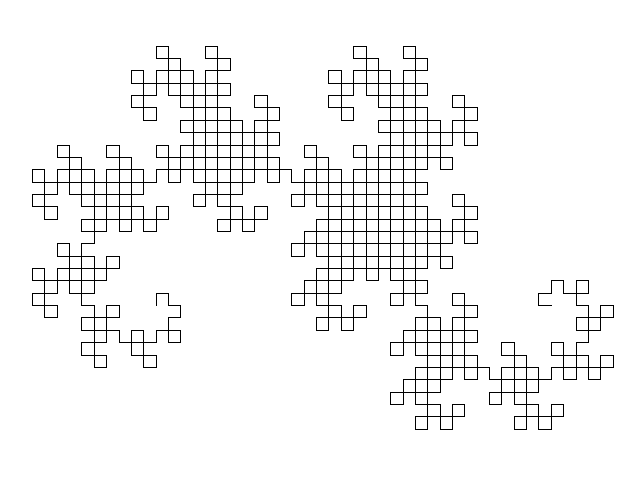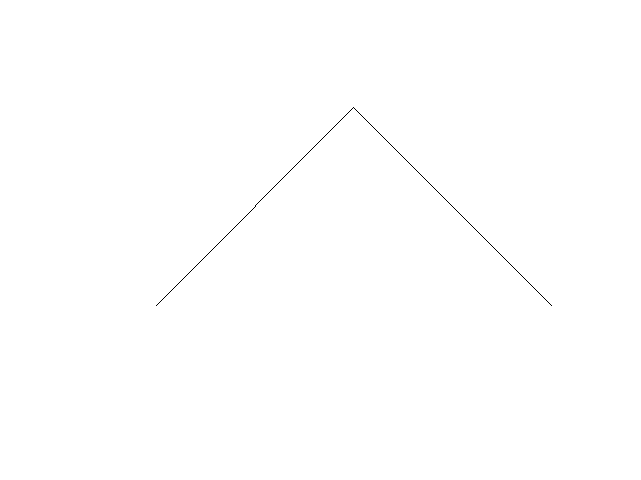
A fractal obtida chama-se de curva do dragão.
A imagem seguinte, também retirado do Wikipédia) mostra como obter uma configuração a partir da anterior.
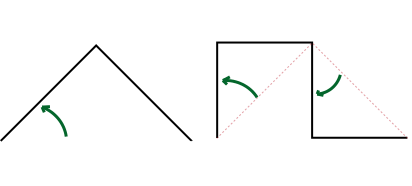
Vamos codificar estas figuras com palavras binárias. O princípio é quando se "um ângulo para a esquerda é 1" e "um ângulo a direita é 0". Assim:
- A fita com zero dobras é representada pela palavra vazia, .
- A fita com uma dobra no meio é codificada pela palavra .
- A fita com duas dobras no meio é codificada pela palavra
- A fita com três dobras no meio é codificada pela palavra
Neste exercício estamos interessado em responder a duas perguntas: qual é a palavra obtida apos n dobras? qual é o m-ésima letra da palavra? Para responder, vamos programar.
Define uma função
dragon_size: int -> intque devolve o tamanho da palavra apos (dado em parâmetro, inteiro positivo, eventualmente nulo) dobras no meio. Por exemplodragon_size 4 = 15.No caso de um argumento inválido, a exceção
Invalid_argument "dragon_size"é lançada.Define uma função
dragon: int -> bool listque devolve a lista dos booleanos que formam a palavra da curva do dragão para n (em parâmetro) dobras.Por exemplo
dragon 3 = [false;false;true;false;false;true;true].No caso de um argumento inválido, a exceção
Invalid_argument "dragon"é lançada.define a função
dragon_bit : int -> boolque para um parâmetro inteiro positivo não nulo devolve o -ésimo bit da sequência do dragão. Por exemplodragon_bit 11 = true.No caso de um argumento inválido, a exceção
Invalid_argument "dragon_bit"é lançada.
Ex. As Torres de Hanói.
Exploremos aqui outro exemplo clássico dos jogos recursivos, as famosas torres de Hanói.
O jogo apresenta-se desta forma:
o tabuleiro tem 3 tores de madeira. Na configuração inicial, a torre da esquerda tem vários discos empilhados ordenadamente do maior ao menor. O jogo consiste em deslocar um a um estes discos seguindo escrupulosamente regras simples que enunciamos a seguir por forma a obter a mesma pilha de discos do que a configuração inicial, mas na torre à direita. Por exemplo, a imagem mostra a configuração inicial, uma configuração intermédia e a configuração final, que significa a vitória. A torre do meio poderá ser usada como recurso intermédio para a estratégia de deslocação dos discos de um lado para o outro.

As regras do jogo são:
- Só podemos deslocar os discos que se encontram no topo de um empilhamento
- Só podemos colocar um disco num empilhamento se este for de tamanho menor do que o disco que se encontra no topo.
Por exemplo na configuração intermédia apresentada na imagem, se quisermos mexer no empilhamento a esquerda, pela primeira regra, só poderemos tirar o circulo de cima. Pela segunda regra ele não poderá ser colocado em nenhuma das duas outras torres. Porque é maior do que os discos que estão no topo de cada uma das torres em questão.
- Defina uma função
hanoi : int -> unitque imprime a sequência de movimentos efetuados para ganhar o jogo com um número de discos igual ao parâmetros dado. Assim, a solução ao jogo com 4 discos é calculada pela chamadahannoi 4. Esta chamada a função deve imprimir na saída standard:
xxxxxxxxxx151Desloco um disco de 1 para 22Desloco um disco de 1 para 33Desloco um disco de 2 para 34Desloco um disco de 1 para 25Desloco um disco de 3 para 16Desloco um disco de 3 para 27Desloco um disco de 1 para 28Desloco um disco de 1 para 39Desloco um disco de 2 para 310Desloco um disco de 2 para 111Desloco um disco de 3 para 112Desloco um disco de 2 para 313Desloco um disco de 1 para 214Desloco um disco de 1 para 315Desloco um disco de 2 para 3
Dica: poderá fazer sentido definir uma função auxiliar que tem por assinatura hannoi_aux : int -> int int -> int -> int tal que hannoi_aux n t1 t2 t3 significa deslocar o disco n de t1 para t2 usando como torre intermédia a torre t3.